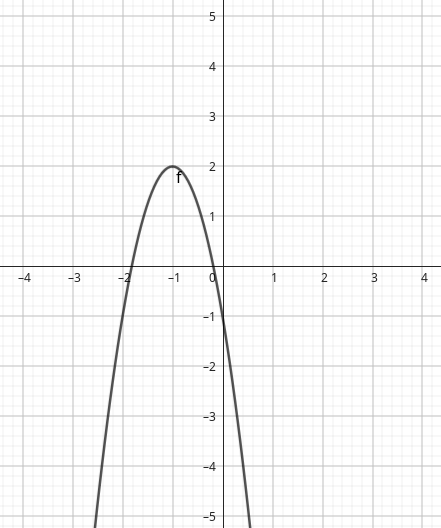
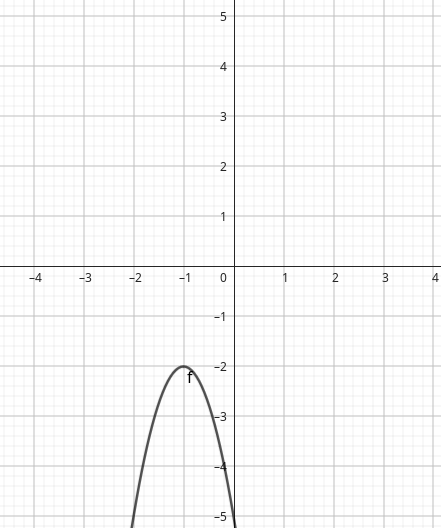
\(a\)
\begin{equation*}
f(x)=a\cdot\left[x^2+\dfrac{b}{a}x+\dfrac{c}{a}\right]
\end{equation*}
\begin{equation*}
f(x)=a\cdot\left[\left(x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}-\dfrac{b^2}{4a^2}+\dfrac{c}{a}\right)\right]
\end{equation*}
\begin{equation*}
f(x)=a\cdot\left[\left(x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}\right)+\dfrac{c}{a}-\dfrac{b^2}{4a^2}\right]
\end{equation*}
\begin{equation*}
f(x)=a\cdot\left[\left(x+\dfrac{b}{2a}\right)^2+\dfrac{c}{a}-\dfrac{b^2}{4a^2}\right]
\end{equation*}
\begin{equation*}
f(x)=a\cdot\left[\left(x+\dfrac{b}{2a}\right)^2+\dfrac{4ac-b^2}{4a^2}\right]
\end{equation*}
\begin{equation*}
f(x)=a\cdot\left(x+\dfrac{b}{2a}\right)^2+\dfrac{4ac-b^2}{4a}\text{,}
\end{equation*}
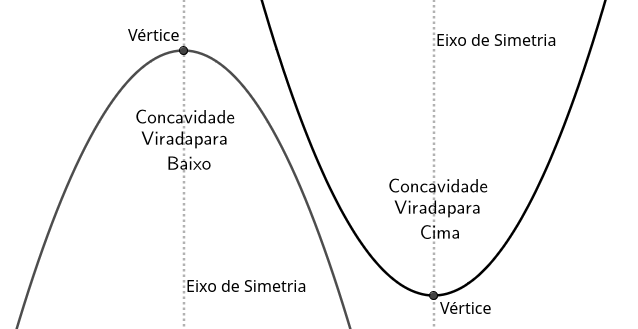
Comparando as funções escritas acima
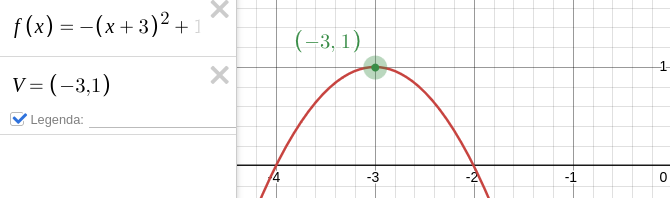
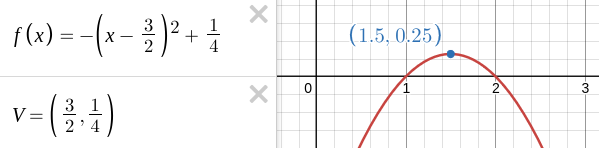
\(f(x)=a(x-m)^2+k\) e
\(f(x)=a\cdot\left(x+\dfrac{b}{2a}\right)^2+\dfrac{4ac-b^2}{4a}\) temos que
\(m=-\dfrac{b}{2a}\) e
\(k=\dfrac{4ac-b^2}{4a}\text{.}\)