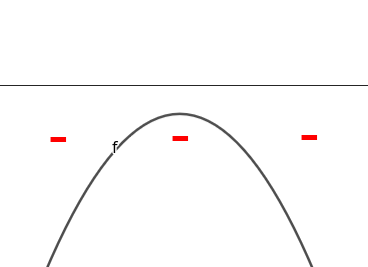
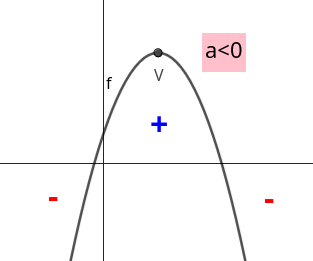
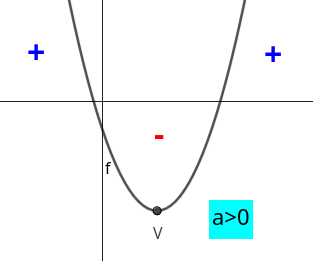
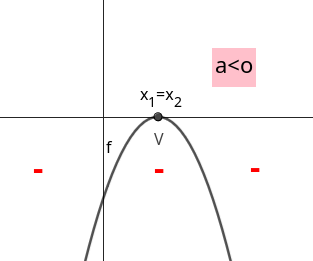
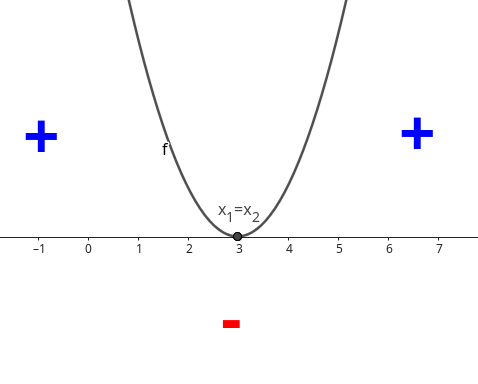
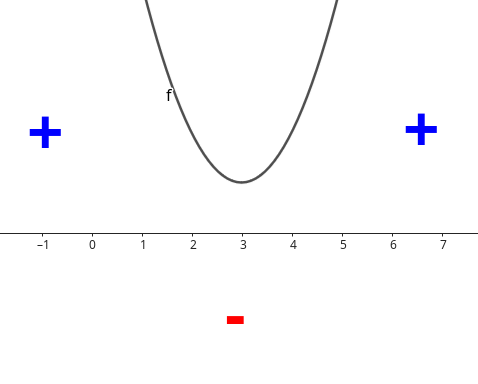
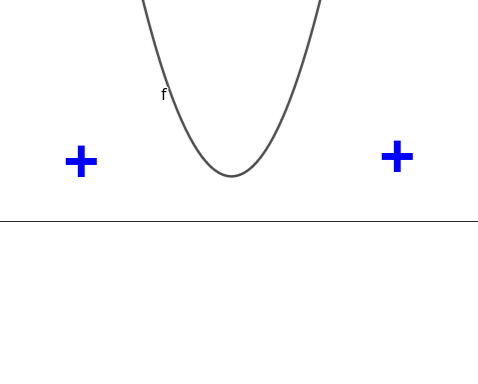
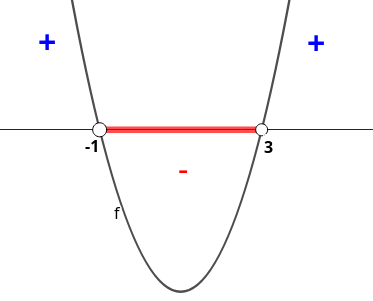
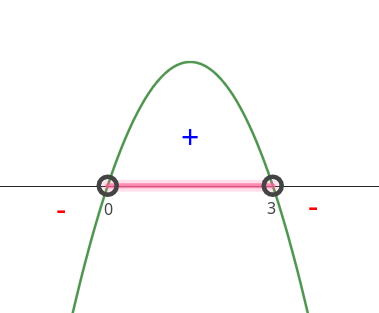
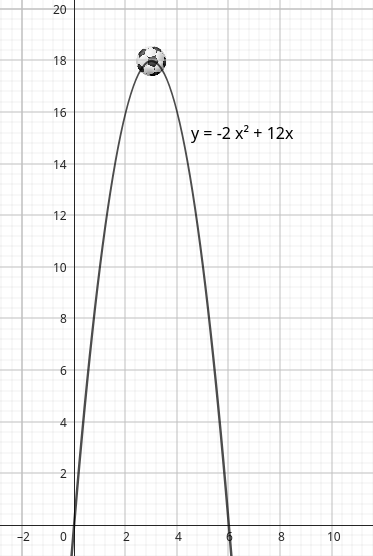
Observaremos agora um outro exemplo, agora com uma função quadrática na forma padrão \(f(x)=-x^2+6x\text{.}\) Calcularemos \(f(x)\) para \(x\in\{-4,-3,-2,-1,0,1,2,3,4,5\}\text{.}\) Mas antes, vamos escrever a função na forma canônica.
\begin{equation*}
f(x)=a(x-m)^2+k=(-1)\cdot \left(x-\dfrac{-6}{2\cdot(-1)}\right)^2+\dfrac{4\cdot (-1)\cdot(0) -6^2}{4\cdot(-1)}
\end{equation*}
\begin{equation*}
=-(x-3)^2+9
\end{equation*}
Logo, temos que \(f(x)=-(x-3)^2+9\text{.}\) Assim:
\begin{align*}
f(-3) \amp =-(-3-3)^2+9=-36+9=-27\\
f(-2) \amp =-(-2-3)^2+9=-25+9=-16\\
f(-1) \amp =-(-1-3)^2+9=-16+9=-7\\
f(0) \amp =-(0-3)^2+9=-9+9=0\\
f(1) \amp =-(1-3)^2+9=-4+9=5\\
f(2) \amp =-(2-3)^2+9=-1+9=8\\
f(3) \amp =-(3-3)^2+9=0+9=9\\
f(4) \amp =-(4-3)^2+9=-1+9=8\\
f(5) \amp =-(5-3)^2+9=-4+9=5
\end{align*}
\((3,9)\)
\begin{align*}
f(3) \amp =9\\
f(2) \amp =f(4)=8\\
f(1) \amp =f(5)=5\\
f(0) \amp =f(6)=0\\
f(-1) \amp =f(7)=-7\\
f(-2) \amp =f(8)=-16\\
f(-3) \amp =f(9)=-27
\end{align*}