Section 3 Projetos
Essa seção reúne projetos utilizando álgebra linear. ** Em construção**
Subsection 3.1 Projeto 1 - Criando uma dieta
Imagine que você é um nutricionista, e precisa prescrever uma dieta para um paciente. Você pode optar por alimentos em uma lista fechada. Os valores nutricionais desses alimentos são conhecidos, e você deve determinar a quantidade de cada alimento a ser consumida diariamente, de modo que, ao fim do dia, o paciente consuma determinada quantidade de cada macronutriente ou substância química presente nos alimentos, como por exemplo gorduras, carboidratos, minerais, proteínas, dentre outros.
Checkpoint 3.1.
Encontre as quantides de fibra alimentar, carboidratos, sódio, proteínas e gorduras totais de 5 alimentos de sua escolha. Para isso, utilize o site https://tabnut.dis.epm.br/alimento
Solution.Arroz, branco, grao longo, normal, cozido
Feijao, preto, semente madura, cozido, sem sal
Frango, carne branca, so carne, pronto para consumo, assado
Alface, crespa, crua
Tomate, vermelho, maduro, cru
| Alimento | Fibra | Carboidratos | Sódio | Proteínas | Gorduras |
| 1 | 0,4 g | 28,17 g | 1 mg | 2,69 g | 0,28 g |
| 2 | 8,7 g | 23,71 g | 1 mg | 8,86 g | 0,54 g |
| 3 | 0 g | 0 g | 51 mg | 27,13 g | 4,07 g |
| 4 | 1,2 g | 2,97 g | 10 mg | 0,9 g | 0,14 g |
| 5 | 1,2 g | 3,89 g | 5 mg | 0,88 g | 0,2 g |
Checkpoint 3.3.
Determine uma quantidade-alvo para cada macronutriente citado e escreva um sistema linear que modele a dieta proposta.
Solution.Fibra alimentar: 20.6 g
Carboidratos: 110.62 g
Sódio: 172 mg
Proteínas: 106.27 g
Gorduras: 14.19 g
Checkpoint 3.4.
Utilize o código na Remark 3.5 para resolver o sistema linear e descobrir as quantidades de cada alimento que o paciente deve consumir.
Solution.200.0 g de Arroz
200.0 g de Feijão
300.0 g de Frango
100.0 g de Alface
100.0 g de Tomate
Remark 3.5.
Código para a resolução de sistemas lineares utilizando o método de Gauss-Jordan.
Checkpoint 3.6.
A solução encontrada faz sentido? Há algo inconveniente ou inadequado na solução? Justifique sua resposta.
Solution.Checkpoint 3.7.
Remova um dos alimentos de sua lista e tente determinar as quantidedes ideais de cada alimento para atingir seus objetivos nutricionais. Qual o resulta obtido? O que você acha que ocorreu?
Solution.Checkpoint 3.8.
Faça uma lista com um total de 7 alimentos e tente determinar as quantidedes ideais de cada alimento para atingir seus objetivos nutricionais. Qual o resulta obtido? O que você faria para obter uma resposta?
Solution.Remark 3.9.
Código para a resolução e otimização de sistemas lineares utilizando o método de Gauss-Jordan. A otimização foi realizada com apoio da biblioteca SciPy, do Python. O programa foi escrito para realizar otimizações com 5 equações e 7 variáveis. Caso deseje fazer com um número diferente, escreva/altere as funções objetivo e as funções limitadoras, conforme explicação e modelo no código.
Subsection 3.2 Projeto 2 - Análise de circuitos resistivos
Em análise de circuitos, utilizamos a Lei de Ohm e as Leis de Kirchhoff de corrente e tensão. Ao encontrar as equações referentes ao circuito utilizando as leis básicas, precisamos montar um sistema linear para encontrar as correntes e quedas de tensão em cada ramo. Analise os circuitos dados utilizando essas três leis, encontre as equações do circuito e forneça-as ao programa em Python disponibilizado ao final da seção para resolver o sistema e encontras as correntes.
Leis básicas:
Lei de Kirchhoff de Corrente: Em qualquer nó, a soma das correntes entrando é igual à soma das correntes saindo.
Lei de Kirchhoff de Tensão: Ao longo de qualquer malha fechada, a soma dos ganhos e das quedas de tensão é igual a zero.
Lei de Ohm: A queda de tensão em um elemento resistivo é dada por \(E = Ri \)
Observe as aplicações das leis básicas nas soluções dos exemplos abaixo.
Example 3.10.
Obtenha as equações referentes à aplicação das leis básicas no seguinte cicuito:
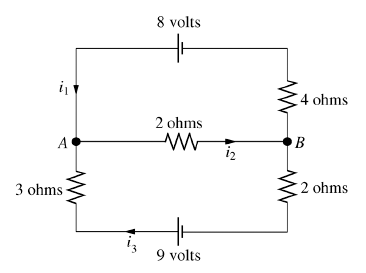
Aplicação da LKC:
Observamos que, no nó A, entram as correntes \(i_1\) e \(i_3\text{,}\) e sai a corrente \(i_2\text{.}\) Por outro lado, no nó B, entra a corrente \(i_2\) e saem as correntes \(i_1\) e \(i_3\text{.}\) Assim, obtemos as equações:
Aplicação da Lei de Ohm:
Aplicando a lei de Ohm, descobrimos que a queda de tensão em cada resistor é:
Resistor de 4 ohms: \(E = 4i_1\)
Resistor de 3 ohms: \(E = 3i_3\)
Resistor de 2 ohms (à esquerda do nó B): \(E = 2i_2\)
Resistor de 2 ohms (abaixo do nó B): \(E = 2i_3\)
Aplicação da LKT:
Aplicando a LKT, obtemos uma equação para cada malha do circuito. Vejamos:
Ao final temos:
Agora basta colocar as equações na forma matricial e fornecer ao programa.
Example 3.12.
Obtenha as equações referentes à aplicação das leis básicas no seguinte cicuito:
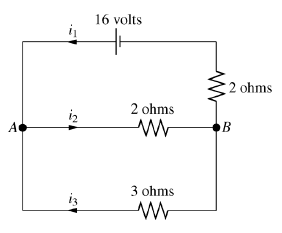
Aplicação da LKC:
Observamos que, no nó A, entram as correntes \(i_1\) e \(i_3\text{,}\) e sai a corrente \(i_2\text{.}\) Por outro lado, no nó B, entra a corrente \(i_2\) e saem as correntes \(i_1\) e \(i_3\text{.}\) Assim, obtemos as equações:
Aplicação da Lei de Ohm:
Aplicando a lei de Ohm, descobrimos que a queda de tensão em cada resistor é:
Resistor de 3 ohms: \(E = 3i_3\)
Resistor de 2 ohms (acima do nó B): \(E = 2i_1\)
Resistor de 2 ohms (à esquerda do nó B): \(E = 2i_2\)
Aplicação da LKT:
Aplicando a LKT, obtemos uma equação para cada malha do circuito. Vejamos:
Ao final temos:
Agora basta colocar as equações na forma matricial e fornecer ao programa.
Example 3.14.
Obtenha as equações referentes à aplicação das leis básicas no seguinte cicuito:
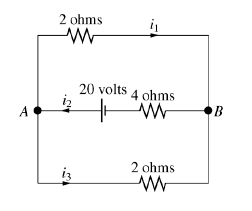
Aplicação da LKC:
Observamos que, no nó A, saem as correntes \(i_1\) e \(i_3\text{,}\) e entra a corrente \(i_2\text{.}\) Por outro lado, no nó B, sai a corrente \(i_2\) e entram as correntes \(i_1\) e \(i_3\text{.}\) Assim, obtemos as equações:
Aplicação da Lei de Ohm:
Aplicando a lei de Ohm, descobrimos que a queda de tensão em cada resistor é:
Resistor de 4 ohms: \(E = 4i_2\)
Resistor de 2 ohms (superior): \(E = 2i_1\)
Resistor de 2 ohms (inferior): \(E = 2i_3\)
Aplicação da LKT:
Aplicando a LKT, obtemos uma equação para cada malha do circuito. Vejamos:
Ao final temos:
Agora basta colocar as equações na forma matricial e fornecer ao programa.
Checkpoint 3.16.
Altere os valores das resistências no circuito abaixo e utilize o seu circuito para obter o sistema de equações referentes à aplicação das leis básicas para as correntes em cada fio (entre nodos):
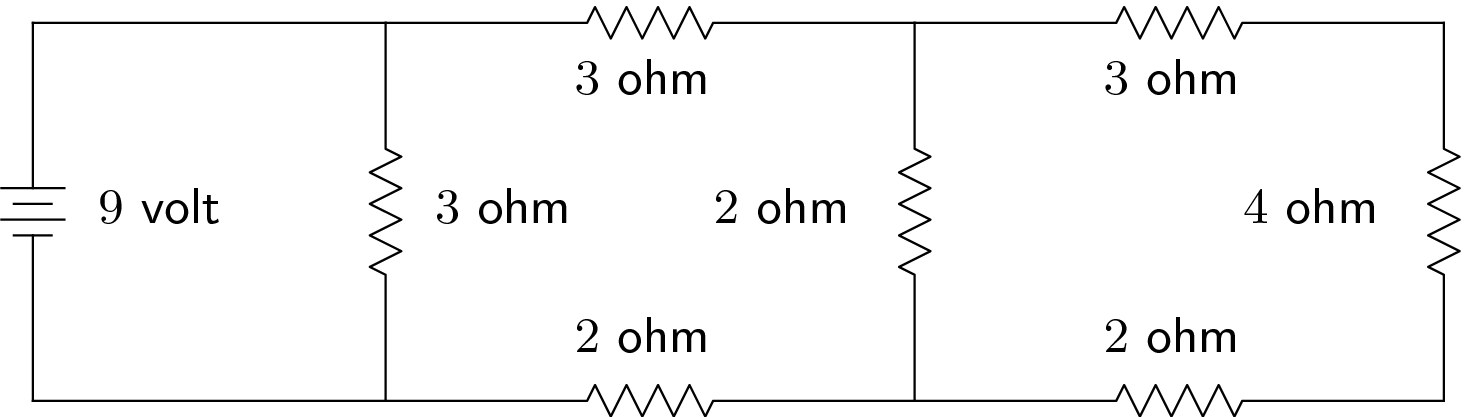
Checkpoint 3.18.
Utilize os códigos em python para resolver o sistema que você criou. Explique como e porque está usando os códigos.
Remark 3.19.
Utilize o código a seguir em Python para avaliar os sistemas lineares obtidos em cada um dos circuitos.Subsection 3.3 Projeto 3 - Ajustando dados aleatórios
Neste projeto, será explorado o método dos quadrados mínimos, método de otimização que tem por objetivo encontrar funções que melhor descrevem um conjunto de pontos em \(\mathbb{R}^n \text{.}\)
Nesta atividade, você deve utilizar um código em python para gerar 10 pontos aleatórios no plano, e depois encontrar as funções linear, quadrática, cúbica e exponencial que melhor se ajustam a esses pontos utilizando o método dos quadrados mínimos. Você pode observar a função que encontrou graficamente e conferir seus resultados utilizando os códigos disponibilizados em cada checkpoint.
Remark 3.20.
Execute este código para gerar seus pontos aleatórios. Você pode modificar os valores mínimo e máximo de x e y. Não altere os valores de N_PONTOS e DISTORCAOCheckpoint 3.21.
Utilizando o método dos quadrados mínimos, ajuste uma função LINEAR aos pontos obtidos. Você pode inserir seus pontos e a função que encontrou no código abaixo para observá-los graficamente e calcular o erro associado à linearização.
Solution.Utilize o código abaixo para conferir sua resposta. Observe o passo a passo da resolução.
Checkpoint 3.22.
Utilizando o método dos quadrados mínimos, ajuste uma função QUADRÁTICA aos pontos obtidos. Você pode inserir seus pontos e a função que encontrou no código abaixo para observá-los graficamente e calcular o erro associado ao ajuste.
Solution.Utilize o código abaixo para conferir sua resposta. Observe o passo a passo da resolução.
Checkpoint 3.23.
Utilizando o método dos quadrados mínimos, ajuste uma função CÚBICA aos pontos obtidos. Você pode inserir seus pontos e a função que encontrou no código abaixo para observá-los graficamente e calcular o erro associado ao ajuste.
Solution.Utilize o código abaixo para conferir sua resposta. Observe o passo a passo da resolução.
Checkpoint 3.24.
Utilizando o método dos quadrados mínimos, ajuste uma função EXPONENCIAL aos pontos obtidos. Você pode inserir seus pontos e a função que encontrou no código abaixo para observá-los graficamente e calcular o erro associado ao ajuste.
Solution.Utilize o código abaixo para conferir sua resposta. Observe o passo a passo da resolução. Lembre-se que os resultados \(c_1\) e \(c_2\) encontrados no vetor solução \(\hat{x}\) gera uma função exponencial da forma \(10^{c_{1} + c_{2}x}\)
Checkpoint 3.25.
Com as 4 curvas encontradas, reflita: Qual é a que melhor se ajusta ao conjunto de pontos que você gerou?
Solution.Insira seus pontos no código abaixo para ver a comparação entre as 4 curvas.
Subsection 3.4 Projeto 4 - Metrologia coordenada
Em diversos processos de fabricação, o controle de qualidade é realizado com auxílio de sensores que detectam pontos do perímetro da peça produzida e comparam estes pontos com o perímetro teórico do objeto.
Neste projeto, suponha que você calculará o fator de erro de cada peça fabricada por uma máquina. As peças devem ter, em teoria, formato circular. Para isso, você deve encontrar, utilizando o método dos quadrados mínimos, a equação da circunferência que melhor se ajusta aos pontos gerados.
Remark 3.26.
Execute o código abaixo para obter os pontos detectados no perímetro da peça fabricada. Não altere os valores de RAIO_MAX e N_PONTOSCheckpoint 3.27.
Encontre o raio e o centro da circunferência que melhor se ajusta aos pontos obtidos. Dica: Monte um sistema com 3 incógnitas
Você pode utilizar o código abaixo para observar graficamente a circunferencia obtida:
Solution.A circunferência com centro em \((c_{1}, c_{2})\) é descrita por \((x-c_{1})^{2} + (y-c_{2})^{2} = R^{2}\text{.}\) Assim:
Os valores de x e y são conhecidos (utilizar as coordenadas dos pontos obtidos). Basta montar o sistema para \(c_1\text{,}\) \(c_2\) e \(c_3\) com \(N\) equações, onde \(N\) é o número de pontos detectados pelo sensor.
Checkpoint 3.28.
Agora encontre o erro associado à fabricação da peça. O erro pode ser descrito como a soma dos módulos de cada vetor \(r\) associado a cada ponto detectado. \(r = R - dist(P, C)\) onde \(P\) é cada ponto que o sensor detectou no perímetro da peça e \(C\) é o centro da circunferência obtida por você. O erro pode ser tomado como uma medida de "quão circular" é o conjunto de pontos.
Solution.Utilize o código abaixo para encontrar o erro associado ao ajuste por quadrados mínimos:
Checkpoint 3.29.
Utilize o código abaixo para conferir suas respostas. Observe o passo a passo da solução.
Subsection 3.5 Projeto 5 - Compressão de imagens quadradas com autovalores e autovetores
Em um computador, uma imagem (em preto e branco) é representada por uma matriz, onde cada valor representa um pixel, isto é, um ponto da imagem. Este valor pode ir de 0 (preto) a 255 (branco). Imagens coloridas são representadas por três matrizes: Uma referente ao canal vermelho (R), outra referente ao canal verde (G) e outra referente ao canal azul (B). Da mesma forma, quando um pixel é representado pelo valor 0 nas três matrizes, temos a cor preta. Quando o pixel é representado pelo valor 255 nas três matrizes, temos a cor branca. Valores intermediários representam ponderações de vermelho, verde e azul, de modo a formar todas as outras cores possíveis. Para transformar uma imagem colorida em uma imagem preta e branca, basta fazer uma média simples entre os elementos \(a_{ij}\) das matrizes R, G e B.
Ao representarmos imagens quadradas como matrizes, podemos extrair seus autovalores e autovetores, obtendo uma base de autovetores para o espaço coluna da matriz da imagem. Neste projeto, será abordado o processo de compressão de imagens utiizando estas características.
Checkpoint 3.30.
Procure uma imagem quadrada (e. g. 1080 x 1080, 400 x 400) qualquer para ver sua representação em três canais. Você deve fornecer ao programa o link de uma imagem.
Observação: Devido a uma trava existente no SageMath (recurso utilizado para executar os códigos no site), o programa não consegue se comunicar com a maioria dos sites. Sabe-se que quaisquer links de imagens da wikipedia (wikimedia) conseguem ser acessados para obter a imagem. Portanto, utilize alguma imagem proveniente de https://commons.wikimedia.org/wiki/Category:Square_images. Se você decidir executar o código diretamente em sua máquina, qualquer link, independente do site de origem, funcionará.
Remark 3.31.
Agora, iremos analisar os autovalores e autovetores associados à matriz da imagem em preto e branco para realizar uma decomposição \(A=PDP^{-1}\text{.}\)
Checkpoint 3.32.
O programa a seguir extrai os autovalores da imagem em preto e branco e os coloca em ordem decrescente de magnitude (norma ou tamanho). Você pode observar graficamente o módulo de cada autovalor, bem como o peso acumulado (soma dos módulos dos primeiros autovalores de 0 a \(n\) dividida pela soma de todos os autovalores). Com base nisso indique, justificando a sua resposta: quantos dos primeiros autovalores você precisaria manter para obter 20% da qualidade da imagem? E 50%? E 90%? Justifique suas respostas.
Solution.Na decomposição \(PDP^{-1}\text{,}\) multilplica-se a matriz \(P\text{,}\) cujas colunas são os autovetores de \(A\text{,}\) pela matriz diagonal \(D\text{,}\) que contem os autovalores da matriz em sua diagonal principal. O produto é, então, multiplicado por \(P^{-1}\text{.}\) Pode-se interpretar o produto \(PD\) como a operação de "esticar" cada autovetor através da multiplicação por seu autovalor correspondente. Nesse contexto, autovalores muito próximos de 0 tem um efeito quase insignificante na matriz final \(A\text{,}\) e por isso, podemos descartá-los, bem como os autovetores associados a eles.
Este processo pode ser usado para comprimir imagens, eliminando uma quantidade significativa da memória utilizada para armazená-la.
Manter apenas os \(r\) autovalores mais significativos da matriz \(A_{n\times n}\) significa remover as colunas \(r+1, r+2, \ldots, n\) da matriz \(P\text{,}\) obtendo uma matriz \(n \times r\text{.}\) Para a matriz \(D\) mantemos apenas as primeiras \(r\) linhas e as primeiras \(r \) colunas, obtendo uma matriz \(r \times r\text{.}\) Para a matriz \(P^{-1}\) mantemos apenas as primeiras \(r\) linhas, obtendo uma matriz \(r \times n\text{.}\)
Checkpoint 3.33.
Agora, execute o código abaixo para visualizar a imagem compactada gerada ao utilizar a decomposição \(PDP^{-1}\) mantendo apenas os primeiros \(r\) autovalores, para os valores escolhidos no checkpoint anterior. Os resultados corresponde ao que você esparava?
Checkpoint 3.34.
Quantas números a matriz da foto original em escala cinza continha? Quantos números têm as matrizes obtidas mantendo apenas \(r\) autovalores para cada um dos três casos que escolheu utilizar? Qual a economia de espaço obtida em cada um dos casos?
Subsection 3.6 Projeto 6 - Compressão de imagens retangulares utilizando SVD
No projeto 5 foi abordada a compressão de imagens quadradas utilizando autovalores e autovetores através da decomposição \(PDP^{-1}\text{.}\) Seria possível realizar uma operação similar para imagens retangulares, representadas por matrizes não quadradas, uma vez que estas não admitem autovalores e autovetores? A resposta é sim! Isto é possível graças a uma técnica amplamente utilizada em processamento digital de imagens: a Decomposição em valores singulares, ou SVD (sigla em ingês).
Remark 3.35.
Para decompor uma matriz \(A_{m\times n}\text{,}\) \(m > n\text{,}\) utilizando SVD, precisamos primeiro calcular duas matrizes: \(AA^T\text{,}\) de ordem \(m\times m\) e \(A^TA\text{,}\) de ordem \(n\times n\)
Observe que estas duas matrizes são simétricas, e portanto possuem \(m\) e \(n\) autovalores reais e distintos, respectivamente. Se ordenarmos estes autovalores, os correspondentes de cada matriz serão iguais, isto é, o autovalor mais significativo de \(A^TA\) é igual ao autovalor mais significativo de \(AA^T\text{,}\) assim como o segundo autovalor mais significativo de cada matriz, e assim em diante.
Definem-se, então, as matrizes \(U\) e \(V\text{:}\)
\(U\) é a matriz \(m\times m\) cujas colunas são os autovetores de \(AA^T\)
\(V\) é a matriz \(n\times n\) cujas colunas são os autovetores de \(A^TA\)
Por fim, define-se uma matriz \(\Sigma _{m\times n}\text{:}\)
Onde cada \(\sigma_i\) é um valor singular de \(A^TA\text{,}\) de modo que \(\sigma_i = \sqrt{\lambda_i}\text{.}\)
Em linhas gerais, \(\Sigma_m\times n\) é uma matriz cujas \(n\) primeiras linhas correspondem a uma matriz diagonal com os valores singulares em sua diagonal principal. Suas \(m-n\) linhas restantes contém somente zeros.
Assim sendo, temos a decomposição em valores singulares de \(A\) como:
Checkpoint 3.36.
Escolha uma imagem retangular para fazer sua decomposição SVD (lembre-se de utilizar uma imagem da Wikimedia). O programa a seguir extrai os valores singulares da imagem em preto e branco e os coloca em ordem decrescente de magnitude (norma ou tamanho). Você pode observar graficamente o módulo de cada valor singular, bem como o peso acumulado (soma dos módulos dos primeiros valores de 0 a \(n\) dividida pela soma de todos os valores). Com base nisso indique, justificando a sua resposta: quantos dos primeiros valores singulares você precisaria manter para obter 20% da qualidade da imagem? E 50%? E 90%? Justifique suas respostas.
De forma análoga à decomposição \(PDP^{-1}\text{,}\) pode-se compactar a imagem ao manter apenas os \(r\) valores singulares mais significativos. Assim, as matrizes passam a ter dimensão \(U_{m\times (r)}\text{,}\) \(\Sigma_{(r)\times r}\) e \({V^T}_{r\times n}\text{.}\)
Checkpoint 3.37.
Agora insira a quantidade de valores singulares que deseja manter para observar a imagem compactada: