Section 1 Sistemas de Equações Lineares
Nessa seção introduzimos sistemas lineares e áplicações práticas. Sistemas lineares são, provavelmente, o tipo de problema matemático mais frequênte em aplicações práticas. Algumas razões para essa afirmação são:
Muitos problemas práticos são lineares por natureza.
A teoria de sistemas lineares permite compreender tais problemas e resolvê-los (equações diferencias, em contra-partida, podem não ser solúveis diretamente).
Métodos computacionais funcionam bem para a solução de problemas lineares.
Problemas mais complexos (como equações diferenciais) podem ser reduzidos a problemas lineares em vários casos de interesse.
Para problemas não lineares, muitas vezes utilizamos aproximações lineares ou métodos que envolvem problemas lineares em diversas etapas de suas soluções.
Subsection 1.1 Sistemas Lineares
Definition 1.1.
Uma equação linear em \(n\) variáveis \(x_1, x_2, \ldots, x_n\) é uma equação da formaExample 1.2.
Example 1.3.
Example 1.4.
Remark 1.5.
Um sistema linear é dito compatível se admite soluções. Sistemas compatíveis podem ter solução única ou infinitas soluções (Não é possível que um sistema linear tenha \(n\) soluções \(n=2, 3, 4, \ldots \) soluções). Um sistema linear é dito incompatível se não admite soluções.Exemplos geométicos são importantes, por exemplo, em computação gráfica. para determinar se algo movendo-se em linha reta (como um projétil em um jogo ou um raio de luz em uma animação *ray tracing) precisamos calcular o ponto de interseção de uma reta com um triângulo (pedaço de plano).
Checkpoint 1.6.
Considere as retas dadas pelas equações:
2y-3x =1,
y + 2x =2,
-2y-4x =a,
encontre os pontos de interseção dos pares de retas 1. e 2.; 2. e 3. para \(a = 0\) e 2. e 3. para \(a = -4\text{.}\)
Checkpoint 1.7.
Utilize o código abaixo para plotar as retas do exercício Checkpoint 1.6.
Checkpoint 1.8.
Utilize o código abaixo para verificar se as soluções encontradas no Checkpoint 1.6 estão corretas.
Os pontos \((x,y,z) \in \mathbb{R}^3\) que estão em um plano no espaço pode ser determinado pelo vetor normal ao plano \(\vec{n} = (n_1, n_2, n_3)\) e por um ponto \(P = (p_1, p_2, p_3)\) satisfazem a equação:
Example 1.9.
Podemos tentar o processo contrário: dada uma equação como determinar o plano que contém todas as soluções? Considerando uma equação da forma
sabemos que o vetor normal é \(\vec{n} = (a,b,c)\) e podemos usar como ponto do plano qualquer valores \(x,y,z\) que satisfaçam a equação acima. Se \(c\neq 0\text{,}\) por exemplo, podemos tomar \(P = (0,0,-d/c)\text{.}\)
As soluções de sistemas lineares de três variáveis correspondem a interseções de planos no espaço, podendo ser um plano todo, uma reta, um ponto ou vazio.
Checkpoint 1.10.
Resolva o sistema a seguir manualmente. Em seguida utilize os códigos acima verificar se sua solução está correta e plotar o plano que contém as soluções.
Checkpoint 1.11.
Resolva o sistema a seguir manualmente. Em seguida utilize os códigos acima verificar se sua solução está correta e plotar o plano que contém as soluções.
Remark 1.12.
Dois sistemas lineares são ditos equivalentes se possuem as mesmas soluções. Dado um sistema linear, podemos realizar três tipos de operações em suas linhas para obter sistemas equivalentes:Trocar duas equações de lugar.
Multiplicar uma equação por um número real não nulo.
Substituir uma equação pela soma dela com um múltiplo não nulo de outra equação.
Example 1.13.
Todos os sistemas a seguir são equivalentes.
O último sistema está na forma triangular. Quando um sistema está na forma triângular, podemos determinar determinar o valor de uma variável e substituir seu valor nas outras equações para reduzir o número de variáveis. Repetimos esse processo até resolver o sistema.
Ao resolver um sistema, utilizamos uma variável com coeficiente não nulo em uma equação para remover essa mesma variável das demais equações. Repetimos o processo até ter uma única variável restante em uma das equações. Assim precisamos de pelo menos \(n\) equações para eliminar \(n\) variáveis. Se tivermos mais do que \(n\) equações, podemos chegar a sistemas sem solução. Em muitos problemas reais o foco está em sistemas \(n \times n\text{.}\)
Subsection 1.2 Matrizes representando sistemas lineares
Considere um sistema de equações lineares:
Para resolver o sistema precisamos dos coeficientes de cada variável. As variáveis \(x_1, x_2, \ldots, x_n\) são apenas nomes. Podemos deixar esses nomes de lado e formar matrizes associadas ao sistema.
A matriz de coeficientes do sistema:
\begin{equation*} A = \begin{pmatrix} a_{11} \amp a_{12} \amp \cdots \amp a_{1n}\\ a_{21} \amp a_{22} \amp \cdots \amp a_{2n}\\ \vdots \amp \vdots \amp \ddots \amp \vdots\\ a_{m1} \amp a_{m2} \amp \cdots \amp a_{mn} \end{pmatrix} \end{equation*}O vetor coluna de constantes:
\begin{equation*} \vec{b} = \begin{pmatrix} b_{1}\\ b_{2}\\ \vdots\\ b_{m} \end{pmatrix} \end{equation*}A matriz ampliada do sistema:
\begin{equation*} (A | \vec{b}) = \left(\begin{array}{cccc|c} a_{11} \amp a_{12} \amp \cdots \amp a_{1n} \amp b_1\\ a_{21} \amp a_{22} \amp \cdots \amp a_{2n} \amp b_2\\ \vdots \amp \vdots \amp \ddots \amp \vdots \amp \vdots\\ a_{m1} \amp a_{m2} \amp \cdots \amp a_{mn} \amp b_m \end{array} \right) \end{equation*}
Remark 1.14.
Podemos agregar quaisquer duas matrizes com o mesmo número de linhas. DadasExample 1.15.
No sistema
A matriz de coeficientes do sistema:
O vetor coluna de constantes:
A matriz ampliada do sistema:
Para resolver o sistema linear podemos operar nas linhas da matriz ampliada. Os coeficientes da \(i\)-ésima coluna correspondem aos coeficientes de \(x_i\) nas respectivas equações. Podemos realizar três tipos de operações (operações elementares) nas linhas da matriz ampliada:
Trocar duas linhas de lugar.
Multiplicar uma linha por um número real não nulo.
Substituir uma linha pela soma dela com um múltiplo não nulo de outra linha.
O objetivo dessas operações é colocar a matriz ampliada na forma escada.
Definition 1.16.
Uma matriz está na forma escada se:
o primeiro elemento não nulo de cada linha é 1;
se a linha \(k\) não é nula, o número de zeros no início da linha é menor do que o número de zeros no início da linha \(k-1\text{,}\) \(k \geq 2\text{;}\)
as linhas nulas estão abaixo das demais.
O código a seguir pode ser utilizado para colocar a matriz do Example 1.15 na forma escada utilizando as operações elementares.
Remark 1.17.
A estratégia utilizada para colocar uma matriz na forma escada consiste trocar linhas para ter um elemento não nulo no canto superior esquerdo. Depois dividimoa a linha por esse elemento para que o elemento no canto superior esquerdo seja 1. Em seguida, utilizamos operações elementares do tipo 3. para zerar os elementos das outras linhas naquela coluna.
Em seguida tentamos repetir esse processo para a segunda coluna. Caso todos os elementos da segunda coluna tenham zerado na primeira etapa, partimos para a terceira coluna. Repetimos isso até chegar à última coluna. Esse processo é chamado de eliminação Gaussiana ou de colocar a matriz na forma escada.
Ao colocarmos uma matriz na forma escada, a posição do primeiro elemento não nulo obtido em uma linha é chamado de pivô daquela linha se todos os elementos na mesma coluna e abaixo dele são nulos.
Example 1.18.
Pivôs em diversas linhas:
Após realizarmos a eliminação Gaussiana, podemos fazer a substituição reversa para encontrar os valores das variáveis (podem depender de algumas variáveis livres), iniciando pela última equação e substituindo os valores encontrados nas demais equações. O código abaixo permite fazer isso para uma matriz que já tenha passado pela eliminação Gaussiana.
Example 1.19.
O sistema
Checkpoint 1.20.
Utilize a eliminação Gaussiana seguida da substituição reversa para resolver os sistemas a seguir. Mostre os passos das contas que realizar. Em seguida compare os resultados obtidos com os resultados apresentados pelo computador nos códigos acima.
Sistema 1
\begin{align*} 2x - 2y - 6z\amp= 8,\\ 3x -5y - z \amp= 0. \end{align*}Sistema 2
\begin{align*} x - y \amp= 1,\\ -x -y - z \amp= -1,\\ -y + z \amp= 1. \end{align*}Sistema 3
\begin{align*} x - y + z\amp= 1,\\ -x -y - z \amp= -1,\\ -y + z \amp= 1,\\ -2y + z \amp= 2. \end{align*}Sistema 4
\begin{align*} x - y + z\amp= 1,\\ -x -y - z \amp= -1,\\ -y + z \amp= 1,\\ -2y \amp= 0. \end{align*}
Example 1.21.
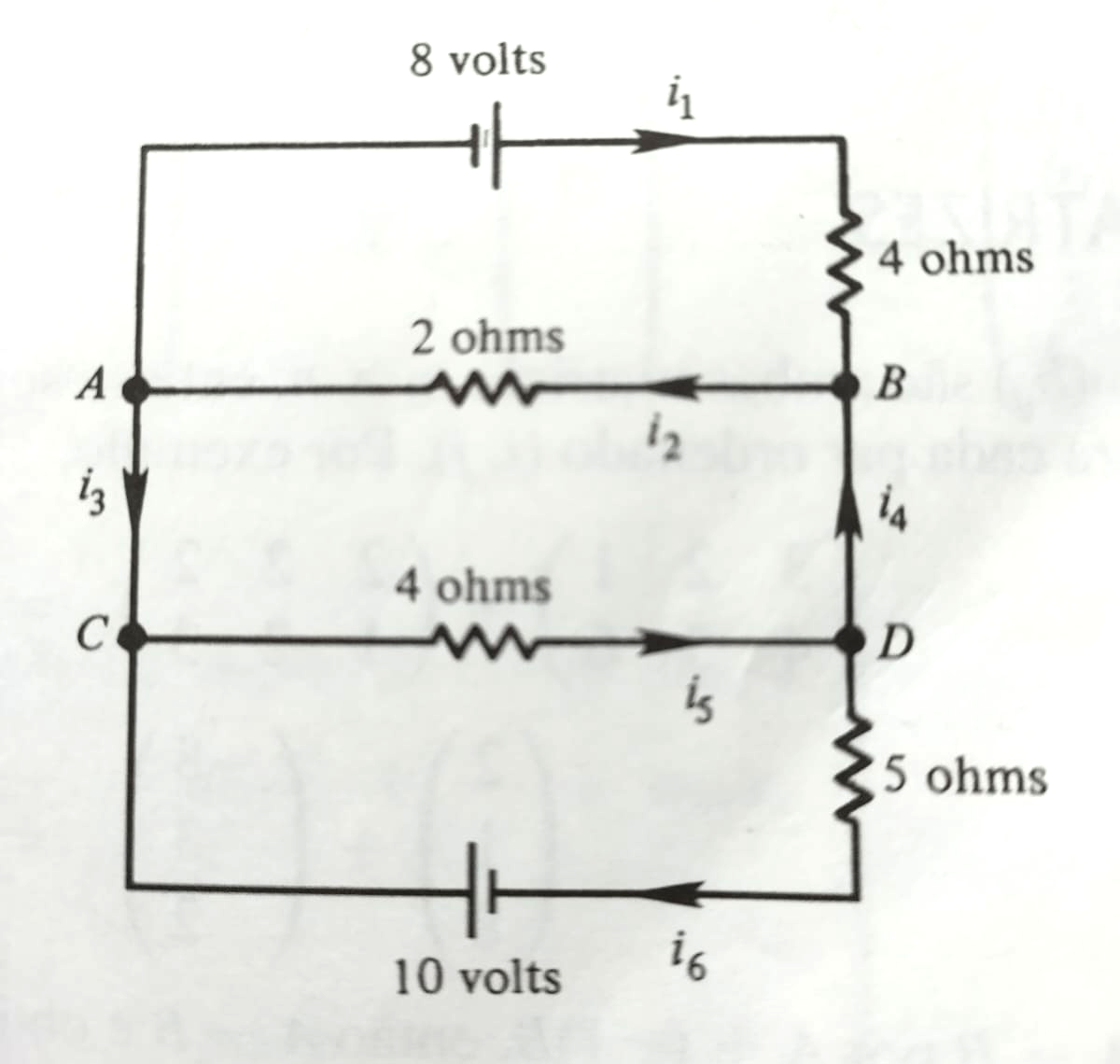
Checkpoint 1.22.
Encontre as correntes \(i_1, i_2, \ldots, i_6\) no circuito da imagem.
Subsection 1.3 Redução de Gauss Jordan
Na seção enterior vimos como utilizar a eliminação Gaussiana na matriz ampliada de um sistema para colocá-la na forma escada e, em seguida resolver o sistema utilizando substituição reversa. Alternativamente, poderíamos seguir fazendo operações elementares nas linhas da matriz ampliada para zerar coeficientes acima de um pivô.
Example 1.24.
O sistema
Example 1.25.
O sistema
Example 1.26.
O sistema
Definition 1.27.
A matriz \(A\) está na forma escada reduzida por linhas se:
\(A\) está na forma escada;
o único elemento não nulo de uma coluna com um pivô é o elemento na posição do pivô.
Remark 1.28.
Chamamos de redução de Gauss-Jordan o processo de usar operações elementares nas linhas de uma matriz para encontrar uma matriz equivalente por linhas na forma escada reduzida por linhas.Example 1.29.
As matrizes a seguir estão na forma escada reduzida por linhas:
Example 1.30.
As matrizes a seguir não estão na forma escada reduzida por linhas:
Checkpoint 1.31.
O diagrama abaixo representa o fluxo de veículos em algumas ruas de uma cidade. Os círculos azuis representam cruzamentos. Os números e variáveis (\(x_1, \ldots, x_5\)) representam a quantidade de carros entrando e saindo dos cruzamentos mostrados (em carros por hora). O número de carros que entra (por hora) em cada cruzamento é igual ao número de carros que sai.
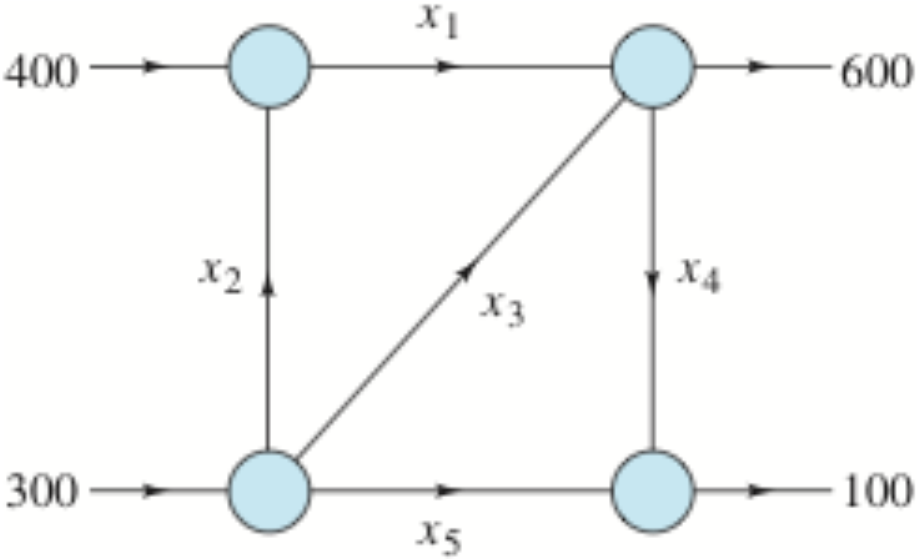
Escreva um sistema que represente o diagrama.
Resolva o sistema encontrado utilizando a redução de Gauss-Jordan.
Determine o fluxo em cada rua para \(x_3 = x_5 =50\text{.}\)
Se a entrade de carros no cruzamento inferior esquerdo mudar para 200 carros por hora e no ccanto superior direito para 500 carros por hora, qual o valor dos demais fluxos (mantendo \(x_3=x_5=50\)).
Refaça o item anterior para o caso de revertermos a direção de \(x_3\text{.}\)
Checkpoint 1.33.
Encontre matrizes equivalentes por linha às matrizes seguintes, que estejam na forma escada reduzida por linhas.